This morning’s weather forecast includes this section:
.WEDNESDAY...CLOUDY. A CHANCE OF SNOW IN THE MORNING...THEN SNOW LIKELY IN THE AFTERNOON. SNOW ACCUMULATION OF 1 TO 2 INCHES. HIGHS AROUND 40. WEST WINDS INCREASING TO 15 TO 20 MPH.
.WEDNESDAY NIGHT...CLOUDY. SNOW LIKELY IN THE EVENING...THEN A CHANCE OF SNOW AFTER MIDNIGHT. LOWS IN THE 20S. WEST WINDS TO 20 MPH DIMINISHING.
Here’s a look at how often Fairbanks gets two or more inches of snow later than April 23rd:
| Date | Snow (in) | Date | Snow (in) |
|---|---|---|---|
| 1915‑04‑27 | 2.0 | 1964‑05‑13 | 4.5 |
| 1916‑05‑03 | 2.0 | 1968‑05‑11 | 2.7 |
| 1918‑04‑26 | 4.1 | 1982‑04‑30 | 2.8 |
| 1918‑05‑15 | 2.0 | 1992‑05‑12 | 9.4 |
| 1923‑05‑03 | 3.0 | 2001‑05‑04 | 3.2 |
| 1931‑05‑06 | 2.0 | 2001‑05‑05 | 2.9 |
| 1948‑04‑26 | 4.0 | 2002‑04‑25 | 2.0 |
| 1952‑05‑05 | 2.8 | 2002‑04‑26 | 4.4 |
| 1962‑05‑07 | 2.0 | 2008‑04‑30 | 3.4 |
It’s not all that frequent, with only 18 occurrences in the last 98 years, and two of those 18 coming two days in a row. The pattern is also curious, with several in the early 1900s, one or two in each decade until the 2000s when there were several events.
In any case, I’m not looking forward to it. We’ve still got a lot of hardpack on the road from the 5+ inches we got a couple weeks ago and I’ve just started riding my bicycle to work every day. If we do get 2 inches of snow, that’ll slow breakup even more, and mess up the shoulders of the road for a few days.
Next month I’ll be attending a game at Wrigley Field and my brother and I had some discussion about the best strategy for us to meet up somewhere in Chicago after the game. Knowing how long a game could be, and how many people are likely to be crowding the train platforms is useful information that can be inferred from the game data that http://www.retrosheet.org/ collects and distributes.
It’s also a good excuse to fiddle around the the IPython Notebook, pandas and the rest of the Python scientific computing stack.
I downloaded the game log data from http://www.retrosheet.org/gamelogs/index.html using this bash one-liner:
for i in `seq 1871 2012`; \
do wget http://www.retrosheet.org/gamelogs/gl${i}.zip ; \
unzip gl${i}.zip; \
rm gl${i}.zip; \
done
Game Length
Game length in minutes is in column 19. Let’s read it and analyze it with Pandas.
import pandas as pd
import matplotlib.pyplot as plt
import datetime
def fix_df(input_df, cols):
""" Pulls out the columns from cols, labels them and returns
a new DataFrame """
df = pd.DataFrame(index=range(len(input_df)))
for k, v in cols.items():
df[v] = input_df[k]
return df
cols = {0:'dt_str', 2:'day_of_week', 3:'visiting_team',
6:'home_team', 9:'visitor_score', 10:'home_score',
11:'game_outs', 12:'day_night', 13:'complete',
16:'park_id', 17:'attendance', 18:'game_time_min'}
raw_gamelogs = []
for i in range(1871, 2013):
fn = "GL{0}.TXT".format(i)
raw_gamelogs.append(pd.read_csv(fn, header=None, index_col=None))
raw_gamelog = pd.concat(raw_gamelogs, ignore_index=True)
gamelog = fix_df(raw_gamelog, cols)
gamelog['dte'] = gamelog.apply(
lambda x: datetime.datetime.strptime(str(x['dt_str']), '%Y%m%d').date(),
axis=1)
gamelog.ix[0:5, 1:] # .head() but without the dt_str col
| dow | vis | hme | vis | hme | outs | day | park | att | time | dte | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Thu | CL1 | FW1 | 0 | 2 | 54 | D | FOR01 | 200 | 120 | 1871-05-04 |
| 1 | Fri | BS1 | WS3 | 20 | 18 | 54 | D | WAS01 | 5000 | 145 | 1871-05-05 |
| 2 | Sat | CL1 | RC1 | 12 | 4 | 54 | D | RCK01 | 1000 | 140 | 1871-05-06 |
| 3 | Mon | CL1 | CH1 | 12 | 14 | 54 | D | CHI01 | 5000 | 150 | 1871-05-08 |
| 4 | Tue | BS1 | TRO | 9 | 5 | 54 | D | TRO01 | 3250 | 145 | 1871-05-09 |
| 5 | Thu | CH1 | CL1 | 18 | 10 | 48 | D | CLE01 | 2500 | 120 | 1871-05-11 |
(Note that I’ve abbreviated the column names so they fit)
The data looks reasonable, although I don’t know quite what to make of the team names from back in 1871. Now I’ll take a look at the game time data for the whole data set:
times = gamelog['game_time_min']
times.describe()
count 162259.000000 mean 153.886145 std 74.850459 min 21.000000 25% 131.000000 50% 152.000000 75% 173.000000 max 16000.000000
The statistics look reasonable, except that it’s unlikley that there was a completed game in 21 minutes, or that a game took 11 days, so we have some outliers in the data. Let’s see if something else in the data might help us filter out these records.
First the games longer than 24 hours:
print(gamelog[gamelog.game_time_min > 60 * 24][['visiting_team',
'home_team', 'game_outs', 'game_time_min']])
print("Removing all NaN game_outs: {0}".format(
len(gamelog[np.isnan(gamelog.game_outs)])))
print("Max date removed: {0}".format(
max(gamelog[np.isnan(gamelog.game_outs)].dte)))
visiting_team home_team game_outs game_time_min
26664 PHA WS1 NaN 12963
26679 PHA WS1 NaN 4137
26685 WS1 PHA NaN 16000
26707 NYA PHA NaN 15115
26716 CLE CHA NaN 3478
26717 DET SLA NaN 1800
26787 PHA NYA NaN 3000
26801 PHA NYA NaN 6000
26880 CHA WS1 NaN 2528
26914 SLA WS1 NaN 2245
26921 SLA WS1 NaN 1845
26929 CLE WS1 NaN 3215
Removing all NaN game_outs: 37890
Max date removed: 1915-10-03
There’s no value for game_outs, so there isn’t data for how long the game actually was. We remove 37,890 records by eliminating this data, but these are all games from prior to the 1916 season, so it seems reasonable:
gamelog = gamelog[pd.notnull(gamelog.game_outs)]
gamelog.game_time_min.describe()
count 156639.000000 mean 154.808975 std 32.534916 min 21.000000 25% 133.000000 50% 154.000000 75% 174.000000 max 1150.000000
What about the really short games?
gamelog[gamelog.game_time_min < 60][[
'dte', 'game_time_min', 'game_outs']].tail()
dte game_time_min game_outs
79976 1948-07-02 24 54
80138 1948-07-22 59 30
80982 1949-05-29 21 42
113455 1971-07-30 48 27
123502 1976-09-10 57 30
Many of these aren’t nine inning games because there are less than 51 outs (8 innings for a home team, 9 for the visitor in a home team win ✕ 3 innings = 51). At the moment, I’m interested in looking at how long a game is likely to be, rather than the pattern of game length over time, so we can leave these records in the data.
Now we filter the data to just the games played since 2000.
twenty_first = gamelog[gamelog['dte'] > datetime.date(1999, 12, 31)]
times_21 = twenty_first['game_time_min']
times_21.describe()
count 31580.000000 mean 175.084421 std 26.621124 min 79.000000 25% 157.000000 50% 172.000000 75% 189.000000 max 413.000000
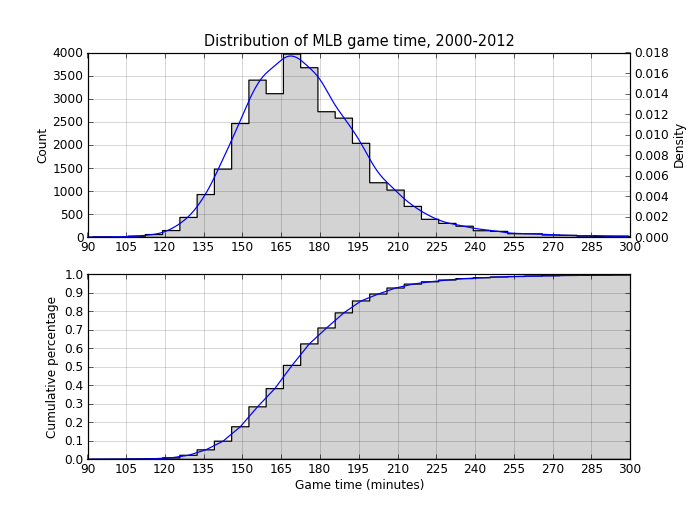
The average game length between 2000 and 2012 is 175 minutes, or just under three hours. And three quarters of all the games played are under three hours and ten minutes.
Here’s the code to look at the distribution of these times. The top plot shows a histogram (the count of the games in each bin) and a density estimation of the same data.
The second plot is a cumulative density plot, which makes it easier to see what percentage of games are played within a certain time.
from scipy import stats
# Calculate a kernel density function
density = stats.kde.gaussian_kde(times_21)
x = range(90, 300)
rc('grid', linestyle='-', alpha=0.25)
fig, axes = plt.subplots(ncols=1, nrows=2, figsize=(8, 6))
# First plot (histogram / density)
ax = axes[0]
ax2 = ax.twinx()
h = ax.hist(times_21, bins=50, facecolor="lightgrey", histtype="stepfilled")
d = ax2.plot(x, density(x))
ax2.set_ylabel("Density")
ax.set_ylabel("Count")
plt.title("Distribution of MLB game times, 2000-2012")
ax.grid(True)
ax.set_xlim(90, 300)
ax.set_xticks(range(90, 301, 15))
# Second plot (cumulative histogram)
ax1 = axes[1]
n, bins, patches = ax1.hist(times_21, bins=50, normed=True, cumulative=True,
facecolor="lightgrey", histtype="stepfilled")
y = n / float(n[-1]) # Convert counts to percentage of total
y = np.concatenate(([0], y))
bins = bins - ((bins[1] - bins[0]) / 2.0) # Center curve on bars
ax1.plot(bins, y, color="blue")
ax1.set_ylabel("Cumulative percentage")
ax1.set_xlabel("Game time (minutes)")
ax1.grid(True)
ax1.set_xlim(90, 300)
ax1.set_xticks(range(90, 301, 15))
ax1.set_yticks(np.array(range(0, 101, 10)) / 100.0)
plt.savefig('game_time.png', dpi=87.5)
plt.savefig('game_time.svg')
plt.savefig('game_time.pdf')
The two plots show what the descriptive statistics did: 70% of games are under three hours but it’s not uncommon for games to last three hours and fifteen minutes. Beyond that, it’s pretty uncommon.
Change in game times in the last 100 years
Now let’s look at how game times have changed over the years. First we eliminate all the games that weren’t complete in 51 or 54 innings to standardize the “game” were’re evaluating.
nine_innings = gamelog[gamelog.game_outs.isin([51, 54])]
nine_innings['year'] = nine_innings.apply(lambda x: x['dte'].year, axis=1)
nine_groupby_year = nine_innings.groupby('year')
mean_time_by_year = nine_groupby_year['game_time_min'].aggregate(np.mean)
fig = plt.figure()
p = mean_time_by_year.plot(figsize=(8, 4))
p.set_xlim(1915, 2015)
p.set_xlabel('Year')
p.set_ylabel('Game Time (minutes)')
p.set_title('Average MLB nine-inning game time since 1915')
p.set_xticks(range(1915, 2016, 10))
plt.savefig('game_time_by_year.png', dpi=87.5)
plt.savefig('game_time_by_year.svg')
plt.savefig('game_time_by_year.pdf')
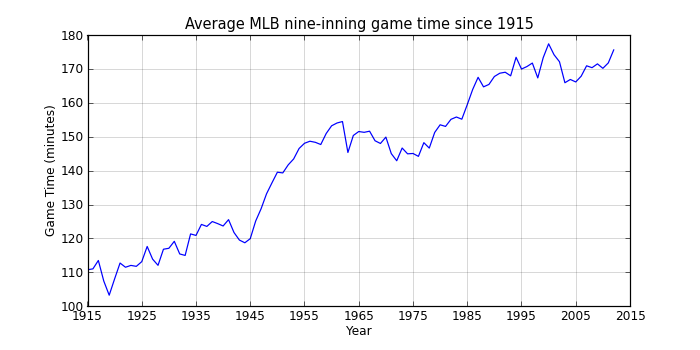
That shows a pretty clear upward trend interrupted by a slight decline between 1960 and 1975 (when offense was down across baseball). Since the mid-90s, game times have hovered around 2:50, so maybe MLB’s efforts at increasing the pace of the game have at least stopped what had been an almost continual rise in game times.
Attendance
I’ll be seeing a game at Wrigley Field, so let’s examine attendance at Wrigley.
Attendance is field 17, “Park ID” is field 16, but we can probably use Home team (field 6) = “CHN” for seasons after 1914 when it opened.
twenty_first[twenty_first['home_team'] == 'CHN']['attendance'].describe()
count 1053.000000 mean 37326.561254 std 5544.121773 min 0.000000 25% 36797.000000 50% 38938.000000 75% 40163.000000 max 55000.000000
We see the minimum is zero, which may indicate bad or missing data. Let’s look at all the games at Wrigley with less than 10,000 fans:
twenty_first[(twenty_first.home_team == 'CHN') &
(twenty_first.attendance < 10000)][[
'dte', 'visiting_team', 'home_team', 'visitor_score',
'home_score', 'game_outs', 'day_night', 'attendance',
'game_time_min']]
| dte | vis | hme | vis | hme | outs | day | att | game_time | |
|---|---|---|---|---|---|---|---|---|---|
| 172776 | 2000-06-01 | ATL | CHN | 3 | 5 | 51 | D | 5267 | 160 |
| 173897 | 2000-08-25 | LAN | CHN | 5 | 3 | 54 | D | 0 | 189 |
| 174645 | 2001-04-18 | PHI | CHN | 3 | 4 | 51 | D | 0 | 159 |
| 176290 | 2001-08-20 | MIL | CHN | 4 | 7 | 51 | D | 0 | 180 |
| 177218 | 2002-04-28 | LAN | CHN | 5 | 4 | 54 | D | 0 | 196 |
| 177521 | 2002-05-21 | PIT | CHN | 12 | 1 | 54 | N | 0 | 158 |
| 178910 | 2002-09-02 | MIL | CHN | 4 | 2 | 54 | D | 0 | 193 |
| 181695 | 2003-09-27 | PIT | CHN | 2 | 4 | 51 | D | 0 | 169 |
| 183806 | 2004-09-10 | FLO | CHN | 7 | 0 | 54 | D | 0 | 146 |
| 184265 | 2005-04-13 | SDN | CHN | 8 | 3 | 54 | D | 0 | 148 |
| 188186 | 2006-08-03 | ARI | CHN | 10 | 2 | 54 | D | 0 | 197 |
Looks like the zeros are just missing data because these games have relevant data for the other fields and it’s impossible to believe that not a single person was in the stands. We’ll get rid of them for the attendance analysis.
Now we’ll filter the games so we’re only looking at day games played at Wrigley where the attendance value is above zero, and group the data by day of the week.
groupby_dow = twenty_first[(twenty_first['home_team'] == 'CHN') &
(twenty_first['day_night'] == 'D') &
(twenty_first['attendance'] > 0)].groupby('day_of_week')
groupby_dow['attendance'].aggregate(np.mean).order()
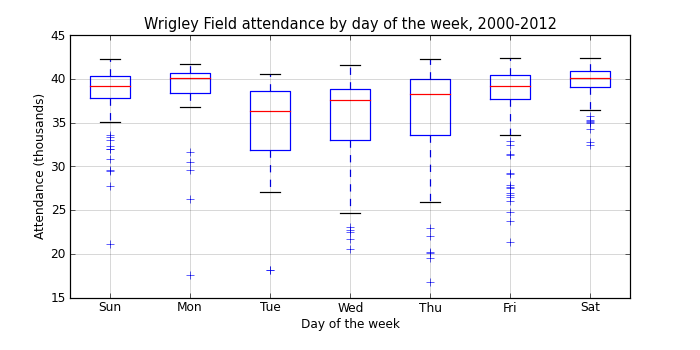
day_of_week Tue 34492.428571 Wed 35312.265957 Thu 35684.737864 Mon 37938.757576 Fri 38066.060976 Sun 38583.833333 Sat 39737.428571 Name: attendance
And plot it:
filtered = twenty_first[(twenty_first['home_team'] == 'CHN') &
(twenty_first['day_night'] == 'D') &
(twenty_first['attendance'] > 0)]
dows = {'Sun':0, 'Mon':1, 'Tue':2, 'Wed':3, 'Thu':4, 'Fri':5, 'Sat':6}
filtered['dow'] = filtered.apply(lambda x: dows[x['day_of_week']], axis=1)
filtered['attendance'] = filtered['attendance'] / 1000.0
fig = plt.figure()
d = filtered.boxplot(column='attendance', by='dow', figsize=(8, 4))
plt.suptitle('')
d.set_xlabel('Day of the week')
d.set_ylabel('Attendance (thousands)')
d.set_title('Wrigley Field attendance by day of the week, 2000-2012')
labels = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
l = d.set_xticklabels(labels)
d.set_ylim(15, 45)
plt.savefig('attendance.png', dpi=87.5)
plt.savefig('attendance.svg') # lines don't show up?
plt.savefig('attendance.pdf')
There’s a pretty clear pattern here, with increasing attendance from Tuesday through Monday, and larger variances in attendance during the week.
It’s a bit surprising that Monday games are as popular as Saturday games, especially since we’re only looking at day games. On any given Monday when the Cubs are at home, there’s a good chance that there will be fourty thousand people not showing up to work!

Cold November
Several years ago I showed some R code to make a heatmap showing the rank of the Oakland A’s players for various hitting and pitching statistics.
Last week I used this same style of plot to make a new weather visualization on my web site: a calendar heatmap of the difference between daily average temperature and the “climate normal” daily temperature for all dates in the last ten years. “Climate normals” are generated every ten years and are the averages for a variety of statistics for the previous 30-year period, currently 1981—2010.
A calendar heatmap looks like a normal calendar, except that each date box is colored according to the statistic of interest, in this case the difference in temperature between the temperature on that date and the climate normal temperature for that date. I also created a normalized version based on the standard deviations of temperature on each date.
Here’s the temperature anomaly plot showing all the temperature differences for the last ten years:
It’s a pretty incredible way to look at a lot of data at the same time, and it makes it really easy to pick out anomalous events such as the cold November and December of 2012. One thing you can see in this plot is that the more dramatic temperature differences are always in the winter; summer anomalies are generally smaller. This is because the range of likely temperatures is much larger in winter, and in order to equalize that difference, we need to normalize the anomalies by this range.
One way to do that is to divide the actual temperature difference by the standard deviation of the 30-year climate normal mean temperature. Because of the nature of the distribution standard deviations are based on, approximately 66% of the variation occurrs within -1 and 1 standard deviation, 95% between -2 and 2, and 99% between -3 and 3 standard deviations. That means that deep red or blue dates, those outside of -3 and 3, in the normalized calendar plot are fairly rare occurrances.
Here’s the normalized anomalies for the last twelve months:
The tricky part in generating either of these plots is getting the temperature data into the right format. The plots are faceted by month and year (or YYYYY-MM in the twelve month plot), so each record needs to have month and year. That part is easy. Each individual plot is a single calendar month, and is organized by day of the week along the x-axis, and the inverse of week number along the y-axis (the first week in a month is at the top of the plot, the last at the bottom).
Here’s how to get the data formatted properly:
library(lubridate)
cal <- function(dt) {
# Reads a date object and returns a tuple (weekrow, daycol)
# where weekrow starts at 1 and daycol starts at 1 for Sunday
year <- year(dt)
month <- month(dt)
day <- day(dt)
wday_first <- wday(ymd(paste(year, month, 1, sep = '-'), quiet = TRUE))
offset <- 7 + (wday_first - 2)
weekrow <- ((day + offset) %/% 7) - 1
daycol <- (day + offset) %% 7
c(weekrow, daycol)
}
weekrow <- function(dt) {
cal(dt)[1]
}
daycol <- function(dt) {
cal(dt)[2]
}
vweekrow <- function(dts) {
sapply(dts, weekrow)
}
vdaycol <- function(dts) {
sapply(dts, daycol)
}
pafg$temp_anomaly <- pafg$mean_temp - pafg$average_mean_temp
pafg$month <- month(pafg$dt, label = TRUE, abbr = TRUE)
pafg$year <- year(pafg$dt)
pafg$weekrow <- factor(vweekrow(pafg$dt),
levels = c(5, 4, 3, 2, 1, 0),
labels = c('6', '5', '4', '3', '2', '1'))
pafg$daycol <- factor(vdaycol(pafg$dt),
labels = c('u', 'm', 't', 'w', 'r', 'f', 's'))
And the plotting code:
library(ggplot2)
library(scales)
library(grid)
svg('temp_anomaly_heatmap.svg', width = 11, height = 10)
q <- ggplot(data = subset(pafg, year > max(pafg$year) - 11),
aes(x = daycol, y = weekrow, fill = temp_anomaly)) +
theme_bw() +
theme(axis.text.x = element_blank(),
axis.text.y = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.ticks.x = element_blank(),
axis.ticks.y = element_blank(),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
legend.position = "bottom",
legend.key.width = unit(1, "in"),
legend.margin = unit(0, "in")) +
geom_tile(colour = "white") +
facet_grid(year ~ month) +
scale_fill_gradient2(name = "Temperature anomaly (°F)",
low = 'blue', mid = 'lightyellow', high = 'red',
breaks = pretty_breaks(n = 10)) +
ggtitle("Difference between daily mean temperature\
and 30-year average mean temperature")
print(q)
dev.off()
You can find the current versions of the temperature and normalized anomaly plots at:

Yesterday I attempted to watch the A’s Opening Day game against the Mariners in the Oakland Coliseum. Unfortunately, it turns out the entire state of Alaska is within the blackout region for all Seattle Mariners games, regardless of where the Mariners are playing.
The A’s lost the game, so maybe I’m not too disappointed I didn’t see it, but for curiousity, let’s extend Major League Baseball’s Alaska blackout “logic” to the rest of the country and see what that looks like.
First, load in the locations of all Major League stadiums into a PostGIS database. There are a variety of sources for this on the Internet, but many are missing the more recent stadiums. I downloaded one and updated those that weren’t correct using information on Wikipedia.
CREATE TABLE stadiums (
division text, opened integer, longitude numeric,
latitude numeric, class text, team text,
stadium text, league text, capacity integer
);
COPY stadiums FROM 'stadium_data.csv' CSV HEADER;
Turn the latitude and longitudes into geographic objects:
SELECT addgeometrycolumn('stadiums', 'geom_wgs84', 4326, 'POINT', 2);
CREATE SEQUENCE stadium_id_seq;
ALTER TABLE stadiums
ADD COLUMN id integer default (nextval('stadium_id_seq'));
UPDATE stadiums
SET geom_wgs84 = ST_SetSRID(
ST_MakePoint(longitude, latitude), 4326
);
Now load in a states polygon layer (which came from: http://www.arcgis.com/home/item.html?id=f7f805eb65eb4ab787a0a3e1116ca7e5):
$ shp2pgsql -s 4269 states.shp | psql -d stadiums
Calculate how far the farthest location in Alaska is to Safeco Field:
SELECT ST_MaxDistance(safeco, alaska) / 1609.344 AS miles
FROM (
SELECT ST_Transform(geom_wgs84, 3338) AS safeco
FROM stadiums WHERE stadium ~* 'safeco'
) AS foo, (
SELECT ST_Transform(geom, 3338) AS alaska
FROM states
WHERE state_name ~* 'alaska'
) AS bar;
miles
------------------
2467.67499410842
Yep. Folks in Alaska are supposed to travel 2,468 miles (3,971,338 meters, to be exact) in order to attend a game at Safeco Field (or farther if they’re playing elsewhere because the blackout rules aren’t just for home games anymore).
Now we add a 2,468 mile buffer around each of the 30 Major League stadiums to see what the blackout rules would look like if the rule for Alaska was applied everywhere:
SELECT addgeometrycolumn(
'stadiums', 'ak_rules_buffer', 3338, 'POLYGON', 2);
UPDATE stadiums
SET ak_rules_buffer =
ST_Buffer(ST_Transform(geom_wgs84, 3338), 3971338);
Here's a map showing what these buffers look like:
Or, shown another way, here’s the number of teams that would be blacked out for everyone in each state. Keep in mind that there are 30 teams in Major League Baseball so the states on the top of the list shouldn’t be able to watch any team if Alaska rules were applied evenly to the country:
| Blacked out teams | States |
|---|---|
| 30 | Alabama, Arkansas, Colorado, Illinois, Indiana, Iowa, Kansas, Kentucky, Louisiana, Michigan, Minnesota, Mississippi, Missouri, Nebraska, New Mexico, North Dakota, Ohio, Oklahoma, South Dakota, Tennessee, Texas, Utah, Wisconsin, Wyoming |
| 29 | Idaho, Montana, Arizona |
| 28 | District of Columbia, West Virginia |
| 27 | Georgia, South Carolina |
| 26 | Nevada |
| 25 | Pennsylvania, Florida, Vermont |
| 24 | Rhode Island, New Hampshire, Connecticut, Delaware, New Jersey, New York, North Carolina, Virginia, Maryland, Massachusetts |
| 23 | Maine |
| 22 | Oregon, Washington, California |
| 1 | Alaska |
| 0 | Hawaii |
Based on this, Hawaii would be the place to live as they can actually watch all 30 teams! Except the blackout rules for Hawaii are even stupider than Alaska: they can’t watch any of the teams on the West Coast. Ouch!
This is stupid-crazy. It seems to me that a more appropriate rule might be buffers that represent a two hour drive, or whatever distance is considered “reasonable” for traveling to attend a game. When I lived in Davis California we drove to the Bay Area several times a season to watch the A’s or Giants play, and that’s about the farthest I’d expect someone to go in order to see a three hour baseball game.
This makes a much more reasonable map:
I’m sure there are other issues going on here, such as cable television deals and other sources of revenue that MLB is trying to protect. But for the fans, those who ultimately pay for this game, the current situation is idiotic. I don’t have access to cable television (and even if I did, I won’t buy it until it’s possible to pick and choose which stations I want to pay for), and I’m more than 2,000 miles from the nearest ballpark. My only avenue for enjoying the game is to pay MLB $130 for a MLB.TV subscription. Which I happily do. Unfortunately, this year I can’t watch my teams whenever they happen to play the Mariners.
Earlier today our monitor stopped working and left us without heat when it was −35°F outside. I drove home and swapped the broken heater with our spare, but the heat was off for several hours and the temperature in the house dropped into the 50s until I got the replacement running. While I waited for the house to warm up, I took a look at the heat loss data for the building.
To do this, I experimented with the “Python scientific computing stack,”: the IPython shell (I used the notebook functionality to produce the majority of this blog post), Pandas for data wrangling, matplotlib for plotting, and NumPy in the background. Ordinarily I would have performed the entire analysis in R, but I’m much more comfortable in Python and the IPython notebook is pretty compelling. What is lacking, in my opinion, is the solid graphics provided by the ggplot2 package in R.
First, I pulled the data from the database for the period the heater was off (and probably a little extra on either side):
import psycopg2
from pandas.io import sql
con = psycopg2.connect(host = 'localhost', database = 'arduino_wx')
temps = sql.read_frame("""
SELECT obs_dt, downstairs,
(lead(downstairs) over (order by obs_dt) - downstairs) /
interval_to_seconds(lead(obs_dt) over (order by obs_dt) - obs_dt)
* 3600 as downstairs_rate,
upstairs,
(lead(upstairs) over (order by obs_dt) - upstairs) /
interval_to_seconds(lead(obs_dt) over (order by obs_dt) - obs_dt)
* 3600 as upstairs_rate,
outside
FROM arduino
WHERE obs_dt between '2013-03-27 07:00:00' and '2013-03-27 12:00:00'
ORDER BY obs_dt;""", con, index_col = 'obs_dt')
SQL window functions calculate the rate the temperature is changing from one observation to the next, and convert the units to the change in temperature per hour (Δ°F/hour).
Adding the index_col attribute in the sql.read_frame() function is very important so that the Pandas data frame doesn’t have an arbitrary numerical index. When plotting, the index column is typically used for the x-axis / independent variable.
Next, calculate the difference between the indoor and outdoor temperatures, which is important in any heat loss calculations (the greater this difference, the greater the loss):
temps['downstairs_diff'] = temps['downstairs'] - temps['outside']
temps['upstairs_diff'] = temps['upstairs'] - temps['outside']
I took a quick look at the data and it looks like the downstairs temperatures are smoother so I subset the data so it only contains the downstairs (and outside) temperature records.
temps_up = temps[['outside', 'downstairs', 'downstairs_diff', 'downstairs_rate']]
print(u"Minimum temperature loss (°f/hour) = {0}".format(
temps_up['downstairs_rate'].min()))
temps_up.head(10)
Minimum temperature loss (deg F/hour) = -3.7823079517
| obs_dt | outside | downstairs | diff | rate |
|---|---|---|---|---|
| 2013-03-27 07:02:32 | -33.09 | 65.60 | 98.70 | 0.897 |
| 2013-03-27 07:07:32 | -33.19 | 65.68 | 98.87 | 0.661 |
| 2013-03-27 07:12:32 | -33.26 | 65.73 | 98.99 | 0.239 |
| 2013-03-27 07:17:32 | -33.52 | 65.75 | 99.28 | -2.340 |
| 2013-03-27 07:22:32 | -33.60 | 65.56 | 99.16 | -3.782 |
| 2013-03-27 07:27:32 | -33.61 | 65.24 | 98.85 | -3.545 |
| 2013-03-27 07:32:31 | -33.54 | 64.95 | 98.49 | -2.930 |
| 2013-03-27 07:37:32 | -33.58 | 64.70 | 98.28 | -2.761 |
| 2013-03-27 07:42:32 | -33.48 | 64.47 | 97.95 | -3.603 |
| 2013-03-27 07:47:32 | -33.28 | 64.17 | 97.46 | -3.780 |
You can see from the first bit of data that when the heater first went off, the differential between inside and outside was almost 100 degrees, and the temperature was dropping at a rate of 3.8 degrees per hour. Starting at 65°F, we’d be below freezing in just under nine hours at this rate, but as the differential drops, the rate that the inside temperature drops will slow down. I'd guess the house would stay above freezing for more than twelve hours even with outside temperatures as cold as we had this morning.
Here’s a plot of the data. The plot looks pretty reasonable with very little code:
import matplotlib.pyplot as plt
plt.figure()
temps_up.plot(subplots = True, figsize = (8.5, 11),
title = u"Heat loss from our house at −35°F",
style = ['bo-', 'ro-', 'ro-', 'ro-', 'go-', 'go-', 'go-'])
plt.legend()
# plt.subplots_adjust(hspace = 0.15)
plt.savefig('downstairs_loss.pdf')
plt.savefig('downstairs_loss.svg')
You’ll notice that even before I came home and replaced the heater, the temperature in the house had started to rise. This is certainly due to solar heating as it was a clear day with more than twelve hours of sunlight.
The plot shows what looks like a relationship between the rate of change inside and the temperature differential between inside and outside, so we’ll test this hypothesis using linear regression.
First, get the data where the temperature in the house was dropping.
cooling = temps_up[temps_up['downstairs_rate'] < 0]
Now run the regression between rate of change and outside temperature:
import pandas as pd
results = pd.ols(y = cooling['downstairs_rate'], x = cooling.ix[:, 'outside'])
results
-------------------------Summary of Regression Analysis-------------------------
Formula: Y ~ <x> + <intercept>
Number of Observations: 38
Number of Degrees of Freedom: 2
R-squared: 0.9214
Adj R-squared: 0.9192
Rmse: 0.2807
F-stat (1, 36): 421.7806, p-value: 0.0000
Degrees of Freedom: model 1, resid 36
-----------------------Summary of Estimated Coefficients------------------------
Variable Coef Std Err t-stat p-value CI 2.5% CI 97.5%
--------------------------------------------------------------------------------
x 0.1397 0.0068 20.54 0.0000 0.1263 0.1530
intercept 1.3330 0.1902 7.01 0.0000 0.9603 1.7057
---------------------------------End of Summary---------------------------------
You can see there’s a very strong positive relationship between the outside temperature and the rate that the inside temperature changes. As it warms outside, the drop in inside temperature slows.
The real relationship is more likely to be related to the differential between inside and outside. In this case, the relationship isn’t quite as strong. I suspect that the heat from the sun is confounding the analysis.
results = pd.ols(y = cooling['downstairs_rate'], x = cooling.ix[:, 'downstairs_diff'])
results
-------------------------Summary of Regression Analysis-------------------------
Formula: Y ~ <x> + <intercept>
Number of Observations: 38
Number of Degrees of Freedom: 2
R-squared: 0.8964
Adj R-squared: 0.8935
Rmse: 0.3222
F-stat (1, 36): 311.5470, p-value: 0.0000
Degrees of Freedom: model 1, resid 36
-----------------------Summary of Estimated Coefficients------------------------
Variable Coef Std Err t-stat p-value CI 2.5% CI 97.5%
--------------------------------------------------------------------------------
x -0.1032 0.0058 -17.65 0.0000 -0.1146 -0.0917
intercept 6.6537 0.5189 12.82 0.0000 5.6366 7.6707
---------------------------------End of Summary---------------------------------
con.close()
I’m not sure how much information I really got out of this, but I am pleasantly surprised that the house held it’s heat as well as it did even with the very cold temperatures. It might be interesting to intentionally turn off the heater in the middle of winter and examine these relationship for a longer period and without the influence of the sun.
And I’ve enjoyed learning a new set of tools for data analysis. Thanks to my friend Ryan for recommending them.